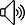对于一个多元函数
![]() ,用最速下降法(又称梯度下降法)求其极小值的迭代格式为
,用最速下降法(又称梯度下降法)求其极小值的迭代格式为
一般情况下,最优步长αkαk的确定要用到线性搜索技术,比如精确线性搜索,但是更常用的是不精确线性搜索,主要是Goldstein不精确线性搜索和Wolfe法线性搜索。
为了调用的方便,编写一个Python文件,里面存放线性搜索的子函数,命名为linesearch.py,这里先只编写了Goldstein线性搜索的函数,关于Goldstein原则,可以参看最优化课本。
线性搜索的代码如下(使用版本为Python3.3):
'''
线性搜索子函数
'''
import numpy as np
import random
def goldsteinsearch(f,df,d,x,alpham,rho,t):
flag=0
a=0
b=alpham
fk=f(x)
gk=df(x)
phi0=fk
dphi0=np.dot(gk,d)
alpha=b*random.uniform(0,1)
while(flag==0):
newfk=f(x+alpha*d)
phi=newfk
if(phi-phi0<=rho*alpha*dphi0):
if(phi-phi0>=(1-rho)*alpha*dphi0):
flag=1
else:
a=alpha
b=b
if(b
上述函数的输入参数主要包括一个多元函数f,其导数df,当前迭代点x和当前搜索方向d,返回值是根据Goldstein准则确定的搜索步长。
我们仍以Rosenbrock函数为例,即有
于是可得函数的梯度为
最速下降法的代码如下:
"""
最速下降法
Rosenbrock函数
函数 f(x)=100*(x(2)-x(1).^2).^2+(1-x(1)).^2
梯度 g(x)=(-400*(x(2)-x(1)^2)*x(1)-2*(1-x(1)),200*(x(2)-x(1)^2))^(T)
"""
import numpy as np
import matplotlib.pyplot as plt
import random
import linesearch
from linesearch import goldsteinsearch
def rosenbrock(x):
return 100*(x[1]-x[0]**2)**2+(1-x[0])**2
def jacobian(x):
return np.array([-400*x[0]*(x[1]-x[0]**2)-2*(1-x[0]),200*(x[1]-x[0]**2)])
X1=np.arange(-1.5,1.5+0.05,0.05)
X2=np.arange(-3.5,2+0.05,0.05)
[x1,x2]=np.meshgrid(X1,X2)
f=100*(x2-x1**2)**2+(1-x1)**2; # 给定的函数
plt.contour(x1,x2,f,20) # 画出函数的20条轮廓线
def steepest(x0):
print('初始点为:')
print(x0,'\n')
imax = 20000
W=np.zeros((2,imax))
W[:,0] = x0
i = 1
x = x0
grad = jacobian(x)
delta = sum(grad**2) # 初始误差
while i
10**(-5):
p = -jacobian(x)
x0=x
alpha = goldsteinsearch(rosenbrock,jacobian,p,x,1,0.1,2)
x = x + alpha*p
W[:,i] = x
grad = jacobian(x)
delta = sum(grad**2)
i=i+1
print("迭代次数为:",i)
print("近似最优解为:")
print(x,'\n')
W=W[:,0:i] # 记录迭代点
return W
x0 = np.array([-1.2,1])
W=steepest(x0)
plt.plot(W[0,:],W[1,:],'g*',W[0,:],W[1,:]) # 画出迭代点收敛的轨迹
plt.show()
为了实现不同文件中函数的调用,我们先用import函数导入了线性搜索的子函数,也就是下面的2行代码
import linesearch
from linesearch import goldsteinsearch
当然,如果把定义goldsteinsearch函数的代码直接放到程序里面,就不需要这么麻烦了,但是那样的话,不仅会使程序显得很长,而且不便于goldsteinsearch函数的重用。
此外,Python对函数式编程也支持的很好,在定义goldsteinsearch函数时,可以允许抽象的函数f,df作为其输入参数,只要在调用时实例化就可以了。与Matlab不同的是,传递函数作为参数时,Python是不需要使用@将其变为函数句柄的。
运行结果为
初始点为:
[-1.2 1. ]
迭代次数为: 1504
近似最优解为:
[ 1.00318532 1.00639618]
迭代点的轨迹为
由于在线性搜索子程序中使用了随机函数,初始搜索点是随机产生的,因此每次运行的结果不太相同,比如再运行一次程序,得到
初始点为:
[-1.2 1. ]
迭代次数为: 1994
近似最优解为:
[ 0.99735222 0.99469882]
所得图像为
以上这篇用Python实现最速下降法求极值的方法就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持脚本之家。